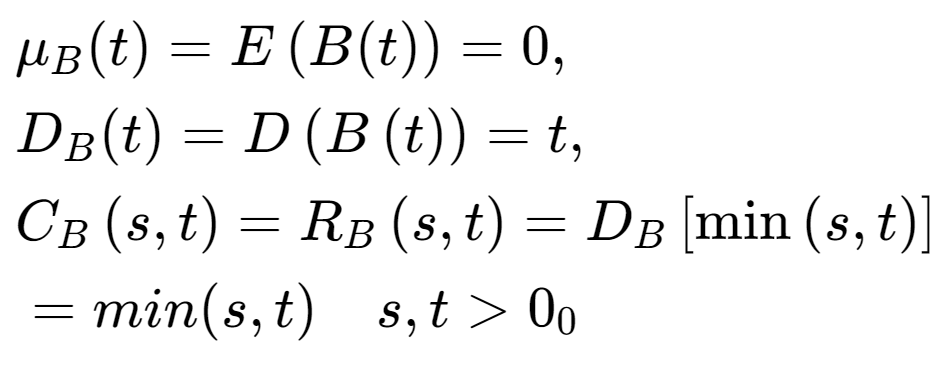随机过程

概统知识点的补充

正态分布

概括一下就是：

服从n元正态分布；每个元素都服从正态分布，且相互独立；其中元素的任意线性组合都服从正态分布。三者是等价的

数字特征

数学期望

协方差函数

随机过程的基本概念

也就是会随着时间变化的随机变量：在某一时刻的随机变量的分布是确定的，但是分布会随着时间参数t变化

（可能是多个随机变量与t构成的函数）

均值函数与协方差函数

随机过程中特别的数字特征主要是自相关函数与自协方差函数（因为时间参数t不同时就是不同的分布）

均值函数：$\mu_X(t)=E[X(t)]$

方差函数：$\sigma_X^2(t)=D_X(t)=D[X(t)]=E[X^2(t)]-E^2[X(t)]$

自相关函数：$R_X(t_1,t_2)=E[X(t_1)·X(t_2)]$

自协方差函数：$C_X(t_1,t_2)=Cov[X(t_1),X(t_2)]=E[X(t_1)·X(t_2)]-E[X(t_1)]·E[X(t_2)]$

互相关函数：$R_{XY}(t_1,t_2)=E[X(t_1)·Y(t_2)]$

互协方差函数：$C_{XY}(t_1,t_2)=Cov[X(t_1),Y(t_2)]=E[X(t_1)·Y(t_2)]-E[X(t_1)]·E[Y(t_2)]$

一些做题的概念：

• 所有的样本函数：就是将其表示成为t的函数（将其余的参数消去）
• 分布律：确定t时的分布
• 求均值函数等时：时间参数t可以看做是常数，可以直接按照运算法则提取出来

正态过程

随机过程在任意不同的时间参数t（$t_1,t_2,…t_n$）下服从n元的正态分布，则称$X(t)$为正态过程

正太过程是二阶矩过程，有限维分布完全由均值函数和自协方差函数确定

相关与独立的关系

马尔科夫链

定义：

将来只有现在的状态决定，现在的结果与过去无关

即知道现在状态的条件下，过去与将来相互独立

$ A=\left{X_{0}=i_{0}, \ldots, X_{n-1}=i_{n-1}\right}, B=\left{X_{n}=i\right}, C=\left{X_{n+1}=j\right} $

转移概率

为m时处于状态i时，n步后转移到状态j的概率

对于时齐的马尔科夫链，$p_{ij}$为从i到j的一步转移矩阵，不依赖于n

常返与暂留

首先来说几个相关的概念吧

1. 首次击中的时间：$\tau_i=min(n\geq1;X_n=i)$ 为首次击中状态 $i$ 的时间（首中时）。

2. 首次击中的概率：$f_{ij}^{(n)}$ 为从状态 $i$ 出发在 $n$ 步首次击中状态 $j$ 的概率。

3. 击中的概率：$f_{ij}=P(\tau_j<\infty\mid X_0=i)$ 为从状态 $i$ 出发在有限步能够击中状态 $j$ 的概率，显然有 $f_{ij}=\sum f_{ij}^{(n)}$ 。

4. 平均回转时：$\mu_i=\sum nf_{ii}^{(n)}=\begin{cases}<\infty\qquad正常返\[2ex]=\infty\qquad零常返\end{cases}$

互达等价类

1. 可达： $i$ 能到达 $j$ 。$i\searrow j$（称为i可达j）。
2. 互达： $i$ 能到达 $j$ 且 $j$ 能到达 $i$ 。$i\leftrightarrow j$ 。有 $d(i)=d(j)$ 且各状态有相同的周期性与常返性。（互达的两个有着相同的周期和常返性）
3. 周期性：

平稳分布

• 定义

  对于时齐的马尔科夫链，设初始的分布为$\pi$，转移矩阵为**$P$**，则$X_1$的分布为$\pi P$，当$X_0与X_1$分布相同时的的$\pi$称为平稳分布（实际上就是马尔科夫链在时间=0时的初始分布）

1. 对于暂留或0常返的状态j：
   1. 对于任意的状态i，$\lim_{n}$

开集和闭集

• 定义：到了闭集之后就出不去了
• 常返与互达等价类是闭集是充要条件

吸收概率与平均吸收时间

• 将马尔科夫链分为暂留态集和若干

定义h为被吸收的概率

泊松过程和纳维过程

独立增量过程

●在互不重叠的区间上,状态的增量是相互独立

泊松过程

以N(t)表示在时间间隔(0,t]内事件发生的数目,N(t),t≥0}是取非负整数、时间连续的随机过程,称为计数过程。

满足以下三个条件的随机过程 ${N(t), t \geq 0}$ 称为参数为 $\lambda$（$\lambda > 0$）的泊松过程：

1. 初始条件：$N(0) = 0$，表示在初始时刻 $t = 0$ 时，事件发生的累计次数为 0。
2. 独立增量性：对任意的 $n$ 以及 $0 \leq t_0 < t_1 < \cdots < t_n$，增量 $N(t_1) - N(t_0), N(t_2) - N(t_1), \cdots, N(t_n) - N(t_{n-1})$ 相互独立。即不相交时间区间上事件发生次数的变化相互独立。
3. 增量分布：对任意的 $t > s \geq 0$，增量 $N(t) - N(s)$ 服从参数为 $\lambda(t - s)$ 的泊松分布，概率质量函数为 $$P(N(t) - N(s) = k) = \frac{(\lambda(t - s))^k e^{-\lambda(t - s)}}{k!}, \quad k = 0, 1, 2, \cdots.$$ 其中 $\lambda$ 为过程的强度，表示单位时间内事件发生的平均次数。

设${N(t),t\geq0}$是计数过程 (满足非负性、单调性、右连左极),若满 足：

1.对充分小的$\Delta t$ ,$P(N(t+\Delta t)-N(t)=1)=\lambda\Delta t+o(\Delta t)$,即在充分小的时间间隔$\Delta t$内，事件发生一次的概率与$\Delta t$成正比，$o(\Delta t)$ 是关于$\Delta t$的高阶无穷小 。

2.对充分小的$\Delta t$ ,$P(N(t+\Delta t)-N(t)\geq2)=o(\Delta t)$ ,即在充分小的时间间隔内，事件发生两次或两次以上的概率是关于$\Delta t$的高阶无穷小，可近似认为几乎不会发生。

3.过程具有平稳独立增量性 (独立增量性同前；平稳增量性指增量 $N(t+h)-N(t)$的分布仅依赖于时间间隔$h$ ,与起始时刻$t$无关 ) ,则称${N(t),t\geq0}$为泊松过程 。

性质：

$\begin{aligned}&1.E\left[N\left(t\right)\right]=\lambda t\&2.D{\left[N(t)\right]}=\lambda t\&3.C_N(s,t)=\lambda min(s,t)\&R_N\left(s,t\right)=C_N\left(s,t\right)+\mu_N\left(s\right)\mu_N\left(t\right)=\lambda min\left(s,t\right)+\lambda^2st,\&s,t\geq0。\end{aligned}$

$5.P{N_{t}=n\mid N_{s}=m}=e^{-\lambda(t-s)}\frac{[\lambda(t-s)]^{n-m}}{(n-m)!}$

使用独立增量性进行解题

将求解的问题转变为求解独立增量的过程，由于是相互独立的，所以可以使用乘法直接展开

合成与分解

合成：

设${N_1(t)}$和${N_2(t)}$是强度为$\lambda_1$和$\lambda_2$的泊松过程，且相互独立，则${N_1(t)+N_2(t)}$是$\lambda_1+\lambda_2$的泊松过程

分解

设${N(t)}$是强度为$\lambda$的泊松过程,若每个事件独立地以概率$p$为类型1,以$1-p$为类型2,令${N_{1}(t)}$和${N_{2}(t)}$分别表示到$t$为止类型1和类型2发生的个数,则${N_{1}(t)}$和${N_{2}(t)}$分别是强度为$\lambda p$和$\lambda(1-p)$的泊松过程,且相互独立.

两个窗口接收服务

非齐次的泊松过程

计数过程$\left{N(t)\right}$称作强度为$\lambda(t)$的非齐次泊松过程，如果

1. $N(0)=0$

2. $\textbf{ 独 立 增 量 }$

3. $P\left { N( t+ h) - N( t) = 1\right } = \overbrace{\lambda ( t) }h+ o( h)$

4. $P{N(t+h)-N(t)\geq2}=o(h)$

上述是非齐次的泊松过程的定义

服从的强度是积分的形式

布朗运动