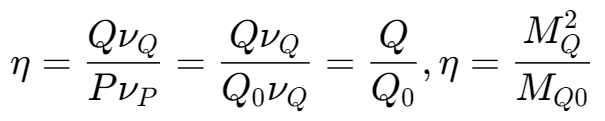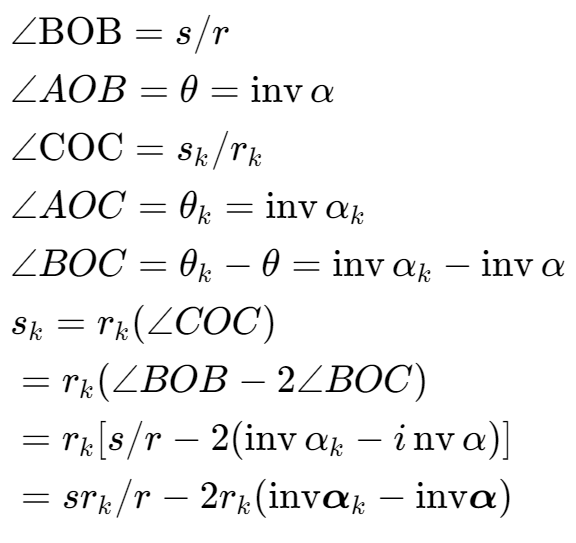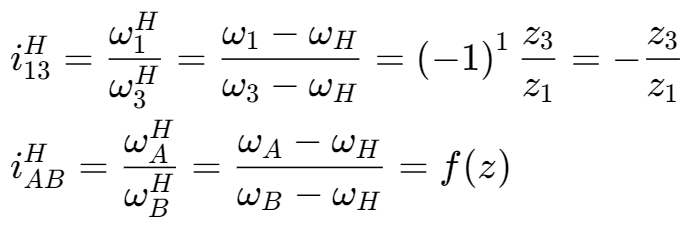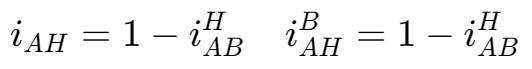平面运动结构分析

副的分类

运动副的分类：

按约束的数目（空间）

1级副：

引入一个几何约束，不能沿着z轴平移
2级副：

4自由度（一个空间自由运动的物体有6个自由度。3动量+3角动量），俩个集合约束
三（罗马数字）级副：

只能旋转，3自由度

平面分类：

平面低副：约束=2,1自由度（名字中的低是低自由度的意思）
1. 回转副（旋转副）
2. 移动副
平面高副：自由度为2，线接触（线约束），常见的为连滚带滑

运动简图和运动示意图：

运动简图：有长度的比例关系
运动示意图：没有表示几何长度，，只说明怎么运动

运动简图的画法：

顺序：

$机架\to主动件\to从动件$

机构自由度的计算

简单结构的公式：

平面：

$$ F=3n-2P_L-P_H $$

公式解释：n为运动部件的数目，不包括机架，机架已经完全限制了

$P_L为低副的数目（回转副和移动副）$

$P_H为高副的数目（线接触）$

特殊的情况：

复合铰链：

一点处有多个回转副时，回转副数目=构件数-1

局部自由度：

凸轮轴顶针的形式

虚约束：

多为三角形和平行四边形
去掉某一个杆不影响其他的平衡和位置
由于几何关系，使得位置已经确定

公共约束：

全是移动副，且至少有三个移动副，失去了一个旋转的自由度

对公式修正

$$ F=2n-P_L $$

易错的模型：

多接触点的滚滑副
有限接触点的回转副和移动副

关键是看实际进行什么样子的约束！

平面机构的高副低代：

圆与圆之间线接触用两个回转副来代替
杆与圆线接触用一个回转副和一个移动副来代替

原则：
1. 自由度不变
2. 运动形式不变

从而实现将所有的高副都转变为低副

拆杆组

机构=机架+主动件+从动件
原则：将从动件拆分出来

步骤：

高副低代，计算自由度

将机架，主动件去除（去除时将副留给从动件）

从远离主动件的地方开始拆，直到$3n=2P_L$

拆成最简的形式

注意

复合铰链有2副，拆走一个还剩一个

移动副画出移动虚线

三角架$\Delta$可以看成一个杆组，因为相对位置已经由几何位置完全确定

平面机构运动分析

速度瞬心法

绝对（相对）瞬心：

瞬时速度为零（相等）的点。
三心定理：

相互作平面运动的三构件间的三个相对瞬心必共线。

俩构件之间的速度瞬心

回转副：在两个构件的接触点（回转轴上）
移动副：在垂直于移动线的无穷远处
纯滚动：接触点
滚滑副：在垂直于公切线的直线上的某一点

特点：

相对速度瞬心绕各自的绝对速度瞬心的$v$相等

两个无限远处的点共的线也在无穷远处

多个构件的速度瞬心：

对于直接接触（直接形成副的构件）：

直接利用上述的俩构件之间的速度瞬心确定速度瞬心
对于非直接接触的构件，使用三心定理：

在两个不同的三心中确定速度瞬心在的直线，直线的交点为速度瞬心
对于杆件数目非常多的机构，使梅花桩的方法：
- 将所有的构件编号画在圆上（包括机架），先将直接接触的瞬心找到，将圆上对应的两个点连起来；
- 再在圆上找一条线（这条线必须为至少两个三角形的公共边），通两个三角形找到速度瞬心

梅花桩

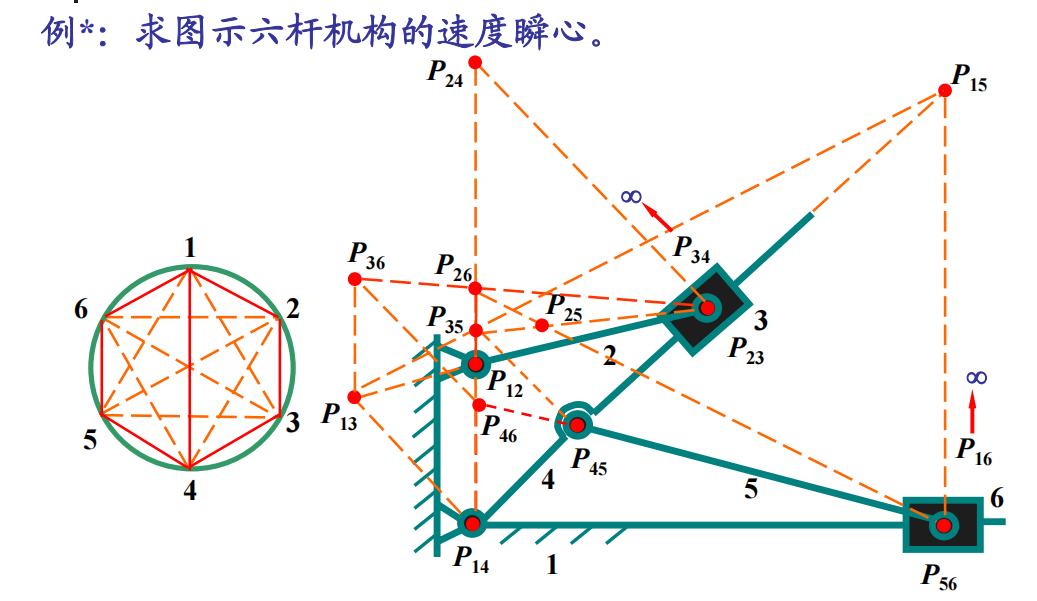
对于移动副的速度瞬心，垂线过的点一般选在杆件（或机架）所在的回转副上

相对运动图解法

同一构件上两点之间的关系

速度：

$$ \begin{array}{c} 矢量式：\quad \boldsymbol{v}_{B}=\boldsymbol{v}_{A}+\boldsymbol{v}_{B A} \\ 方向：\quad\perp B P \quad \perp A P \quad\perp A B \\ 大小：\quad\omega l_{B P} \quad \omega l_{A P}\quad \omega l_{A B} \end{array}\\ 其中P为此构件的绝对速度瞬心点。 $$

加速度：

$$ 矢量方程： \boldsymbol{a}_{B}{ }^{n}+\boldsymbol{a}_{B}{ }^{t}=\boldsymbol{a}_{A}{ }^{n}+\boldsymbol{a}_{A}{ }^{t}+\boldsymbol{a}_{B A}{ }^{n}+\boldsymbol{a}_{B A}{ }^{t} \\ 方向： \quad / / B P \quad \perp B P \quad / / A P \quad \perp A P \quad B \rightarrow A \quad \perp A B \\ 大小： \quad v_{B}^{2} / r_{B}\quad d v_{B} / d t \quad v_{A}^{2} / r_{A} \quad d v_{A} / d t \quad \omega^{2} l_{A B} \quad \alpha l_{A B} \\ 其中 r_{A}=A P_{A}, ~ r_{B}=B P_{B} 为 A, ~ B 在各自轨迹上的曲率半径。 $$

同一构件

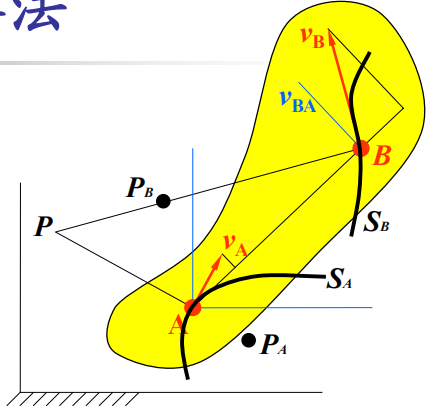
相当与理论力学中的基点法

移动副两构件上瞬时重合点间的运动关系：

速度：

$$ 矢量方程： \boldsymbol{v}_{A 2}=\boldsymbol{v}_{A 1}+\boldsymbol{v}_{21}{ }^{r} \\ 方向： \perp A P_{2} \quad \perp A P_{1} \quad 沿导轨\\ 大小： \quad \omega l_{P 2 A} \quad \omega l_{P 1 A} \quad v_{r} \\ 其中 P_{1} 与 P_{2} 分别为构件 1 与 2 的绝对瞬心点。\\ $$

加速度：

$$ 矢量方程： \boldsymbol{a}_{A 2}{ }^{n}+\boldsymbol{a}_{A 2}{ }^{t}=\boldsymbol{a}_{A 1}{ }^{n}+\boldsymbol{a}_{A 1}{ }^{t}+\boldsymbol{a}_{21}{ }^{k}+\boldsymbol{a}_{21}{ }^{r} \\ 方向： \quad / / A P_{2} \quad \perp A P_{2} \quad / / A P_{1} \quad \perp A P_{1} \quad \perp \boldsymbol{v}_{21}{ }^{r} \quad 沿导轨\\ 大小： \quad v_{A 2}{ }^{2} / r_{A 2} \quad d v_{A 2} / d t \quad v_{A 1}{ }^{2} / r_{A 1} \quad d v_{A 1} / d t \quad 2 \omega v_{r} \quad d v_{l} / d t \\ 其中 r_{A 1}, ~ r_{A 2} 为 A_{1} 与 A_{2} 在各自轨迹上的曲率半径。 $$

可见，由于引入了动系，出现了科氏加速度。

两个构件

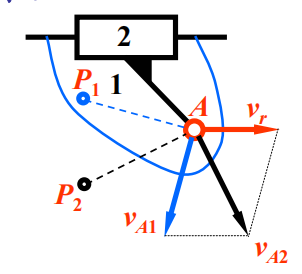
科氏加速度存在与方向的判断

几个典型：

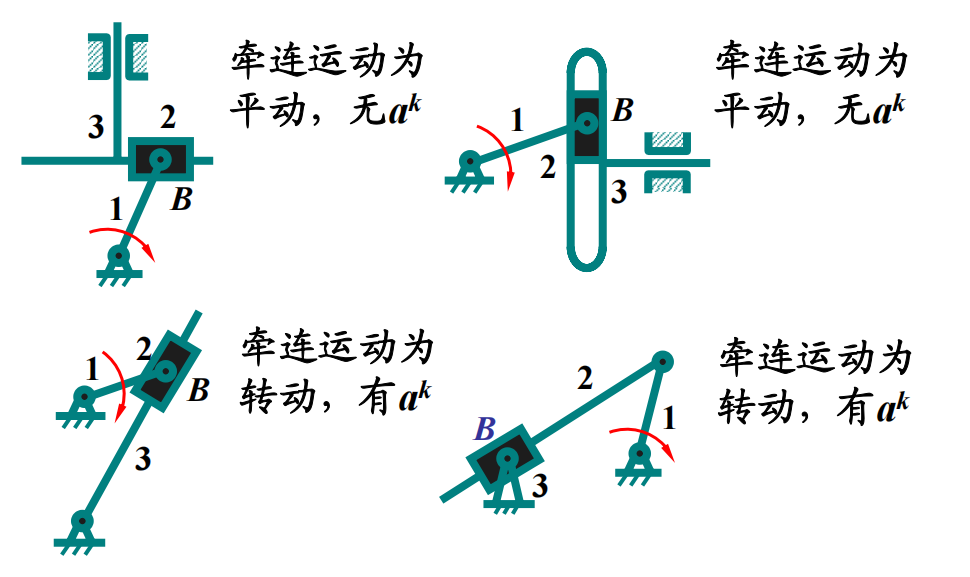
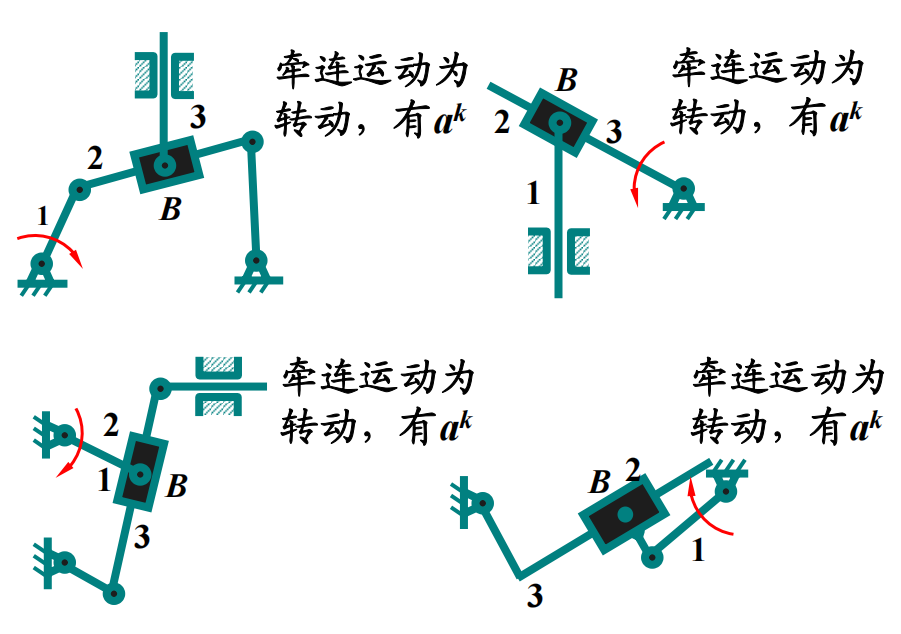
重合点的选取

可以将构件扩大，扩大到速度大小方向好求的点，进行计算

杆与另外一杆刚性连接，可以看做整个杆绕改杆的轴做圆周运动，但是不是刚性连接时不行

步骤：

判断哪个是主动运动

判断哪些是同一个点

哪些是瞬时重合点

确定动点、动系，确定动系有无回转运动

有时会用到同一杆件上不同点的方法逐步解决

图解法：画矢量三角形（为矢量式子）

求杆件速度瞬心的两种方法：

利用三心定理
同一杆件上有两个点的速度方向已知时，可以求出速度瞬心的位置

做题

在一直某一杆件的速度，想要求另一杆件的速度时可以直接找出两者的速度瞬心，利用在两个参考系下的速度瞬心速度相同计算

瞬心法

瞬心：两个构件的瞬时速度相等的点，两个构件上的这个点的绝对速度相等，相对速度为0

先进行瞬心位置的判断（直接接触的杆件和非直接接触的杆件）
求出两个构件之间的瞬心即可通过瞬心与运动关系求解速度和角速度（无法求解加速度）

矢量方程图解法

分为两类：

同一杆件上两点之间的运动关系
两构件重合点之间的运动关系

同一构件上

速度

矢量画图时，取比例尺

确定比例尺之后，从P点开始画的为绝对速度

列出速度关系式，根据大小、方向的已知、未知进行画图

根据画出射线的长度与方向和比例尺，确定待求速度的大小和方向

加速度

同样的比例尺和原点，找一下原（主）动件（告诉初速度的杆件），这一件的切向加速度为0

除了原动件或者是平动的都是有切向和法向加速度的

一般未知的加速度有时不需要拆分的（拆分成切向和法向），当然也是可以拆开的（如果拆开能减少一个未知数时）

利用速度、角速度的关系算出已知的加速度，确定方向

画图（根据比例尺，大小和方向画图），画完之后亮出来根据比例尺即可

两个构件的重合点（可以使用扩大构件的方法进行计算杆件上某一点的速度）

速度：

同样取速度比例尺，先定一个基点P，角标是小写的

此时会有科氏加速度（两个构件的相对运动为移动，牵连运动为转动，两者在重合点便存在科氏加速度，大小为$2wv_r$，角速度×相对速度，大小为将相对速度沿着加速度转90°）和相对加速度

根据比例尺和已知的大小和方向画图，进行计算

$V_{B3}$表示构件3在B点的速度大小

解题时

速度和加速度

首先是根据同一杆件和不同杆件上的速度关系（有时候需要组合使用）能够把一个杆件上的两个点的速度和加速度求出来

之后在一条线上的点的速度也在一条线上，分线段的比例等于杆件上实际的比例，垂直的在速度图像上也是垂直的，比例也是实际的比例

比例是实际的比例，甚至完全是个相似三角形

平面机构的力分析

运动副中的反力

移动副中的反力

对于移动副来说，当滑块在平面上滑动时，会受到支撑反力和摩擦力

摩擦角等于总反力与法向反力之间的夹角

$\varphi=arctanf$：其中的f为摩擦系数

我们使用的是当量摩擦系数

$f_v$：与摩擦面的形状有关

平面接触：

槽接触：

方向已知：摩擦角，但是大小未知
作用点在接触线上，但是具体位置未知
所以有两个未知量

回转副中的反力

轴在轴承中的转动，也是先找一下相对运动的方向

引入一个新的概念：摩擦圆

摩擦圆与与总反力始终相切（过一点做摩擦圆的切线有两个，根据相对运动的方向确定）

摩擦圆的半径使用

$\rho=f_v r$r为轴径半径，使用这个公式计算摩擦圆的半径

总反力必切于摩擦圆
总反力大小与作用点未知

有两个未知量

其中的摩擦圆的半径$\rho=f_vr$

杆组满足静定条件：$3n=2P_L$

力分析的图解法

做摩擦圆
做二力杆的反力的作用线
分析其他的杆件的受力情况

先确定二力杆，因为

二力杆的受力状态，受压还是受拉

二力杆受到的力一定是平行于杆件的

选择哪个公切线的原则：受压还是受拉、需要阻碍相对运动的趋势（对作用点取矩）

再确定其他的

使用受力平衡的方式进行分析

力分析的杆组法

机械的效率

机器的运动：起动+稳定运转+停车

输入功+克服工作阻力所作的有益功+克服摩擦的无用功

$$ A_d=A_r+A_f\\ N_d=N_r+N_f $$

机械效率=有益功/输入功

机械的自锁

由于摩擦力的存在，使得机构自锁

推导反行程的自锁（就是不想出现的工作状态）

移动副：驱动力在摩擦角之内（就是驱动构件运动的力）
还有一种判断方法就是使用生产阻力<=0
- 也就是将所有的力列出来，将生产阻力使用驱动力进行表示，生产阻力是小于等于0的，从而得出条件
自锁是有方向性的，有正行程的自锁和反行程的自锁
还有就是使用效率进行计算
- 效率等于理想的驱动力除以实际的驱动力（理想的就是在没有摩擦的情况下）

受力分析-总反力-矢量图-正弦方程

有正反行程的区分

正行程和反行程的驱动力和工作阻力是交换的

正行程

驱动力使用p表示，工作阻力使用Q表示，两者计算公式的分母是相反的（理想的角标是0）

驱动力就是在这个行程下会做正功的力

反行程

角标上加个*

驱动力和工作阻力恰好和正行程的相反

判别

正常工作两个效率全大于0

自锁反行程的效率<=0

平面连杆机构

连杆机构的特点及设计问题

定义：低副机构
- 面接触

平面四杆机构的型式及演化

分类：（先按照是否含有移动副分类）（再按照含有曲柄与摇杆的数目）

铰链四杆机构

曲柄摇杆、双曲柄**、**双摇杆机构

含一个移动副的四杆机构

曲柄滑块、转动导杆、曲柄摇块、

移动导杆机构

含二个移动副的四杆机构

正弦、双转块、曲柄移动导杆、双滑块

正切、滑块摇杆、摇杆导杆、滑块摇块机构

偏心轮机构：（相当于一个曲柄连杆）

单偏心轮、双偏心轮机构

曲柄：会相对机架做整周期运动（一整个圆）

摇杆：不会做整周期运动

铰链四杆机构：

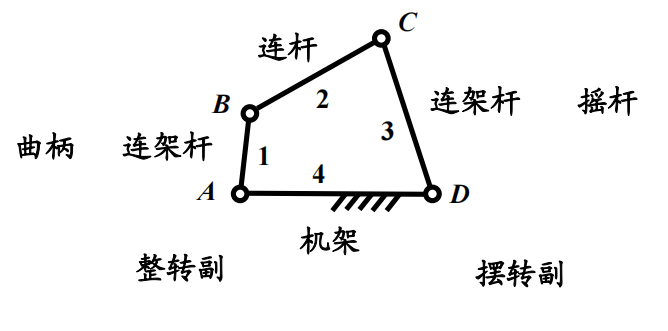
概念辨析

连架杆：与机架直接相连的杆件
连杆：与机架相对的杆件

整转副：有曲柄的机构
摆转副：只有摇杆的机构

将一个摆转副转变成移动副

将第二个摆转副转变成移动副

平面四杆机构的运动特性

铰链四杆机构中整转副的充要条件：

必要条件：

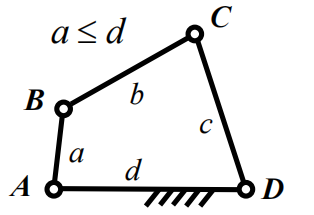
最短边与最长边长度之和不大于另外两边的长度之和。称为杆长条件。是铰链四杆机构存在整转副的必要条件。

假设b为最长边，a为最短边，则必要条件是$a+b\leq c+d$

铰链四杆机构中某回转副成为整转副充要条件：
- 各杆长度满足杆长条件。
- 构成此回转副的两构件中有一个为最短构件。

平面四杆机构的运动特性

急回特性与行程速比系数 K：
- $$ K=\frac{180^{\circ}+\theta}{180^{\circ}-\theta} \quad \theta=\frac{K-1}{K+1} 180^{\circ} $$
  此处的$\theta$为极位夹角（是机构的摇摆副或移动副在极限位置时的角度）
压力角与传动角：
- $$ \alpha+\gamma=90°\\ $$
  其中前者为压力角（受力与运动方向的夹角）
  
  后者为传动角（利用说明力对速度大小的贡献）
死点位置：
- 当力与杆件的运动方向垂直时，$\gamma$角=0，力对杆件的速度不起作用。此时若杆件的速度为0，机构将不再运动

平面四杆机构的设计

实现连杆给定位置

连杆长度已知，机架长度待求
- 两位置问题设计
- 三位置问题设计
  已知B、C在三种情况下的位置（$B_1,B_2.B_3.C_1,C_2,C_3$）,求机架的位置。
  1. 连接$B_1B_2,B_2B_3$，做中垂线，由于是绕着A点旋转的，所以交点为A点所在的位置
  2. 同样的方法求出D点的位置
连杆长度待求，机架长度已知

转换机架法：找出机架相对于连杆的位置序列
原理：由于机构的形状是在不同的杆件为机架的条件下都可以旋转成的，所以说可以以MN（BC）为机架，将不同的形状旋转平移到同一个地方，转换成上述的连杆长度已知
- 已知$M_1N_1.M_2N_2,M_3N_3，MN$为BC杆件上的点，不是绕着A、C旋转的
方法：
1. 将不同形状的机构连接起来，选择一个MN为基准，将其他形状的机构进行旋转和平移，使得MN都相互重合
2. 做A、D的中垂线（看作是连杆），交点为B、C点

实现给定运动规律

两连架杆的对应角位移已知, 旋转法。
- 两组对应角位移。
  已知$A,D,B和\alpha_1,\alpha_2,\varphi_1,\varphi_2.\alpha为不同的AB_i之间所夹的角，\varphi为不同的DC_i之间夹角$
  
  方法：
  1. 转换支架，以CD为支架，假设CD的位置，D的位置是不变的，只有C会绕着转，以CD为支架，就要将AB绕着D点旋转回来，反着转$\varphi_1,\varphi_2$角度
  2. 此时就是以CD为支架，已知A，B的三个位置。过B的做中垂线即可
- 三组对应的角位置
  已知$\alpha，\varphi$的三个角和A,D点的位置，但是B，C的位置都是未知的
  
  方法：
  1. 连接AD并且延长，以这条线为基准，在A处以$\frac{\alpha_1-\alpha_2}{2}$做一条射线，在D处同向以$\frac{\varphi_1-\varphi_2}{2}$的角度做射线，交点就是$B_4$
  2. 通过角度的关系求出B的其余三个位置
  3. 在由之前的做法求即可（为了防止交点不唯一，因为有4个点，旋转之后B有两个点会重合）
- 给定行程比系数K
  已知：D点，C的两个位置，定行程比系数K
  1. 先根据K，求出极位夹角（极位夹角的圆心是曲柄的圆心，端点是摇杆的端点，是摇杆在两个极限位置时的夹角）
  2. 以$C_1,C_2为两点，极位夹角的2倍为顶角做一个三角形，以定点为圆心做一个外接圆则，随便在圆上取一个点为A点$
  3. $AC_1=BC-AB,AC_2=BC+AB$则使用尺规作图（作差，做中垂线为AB的长度，与AC共线）
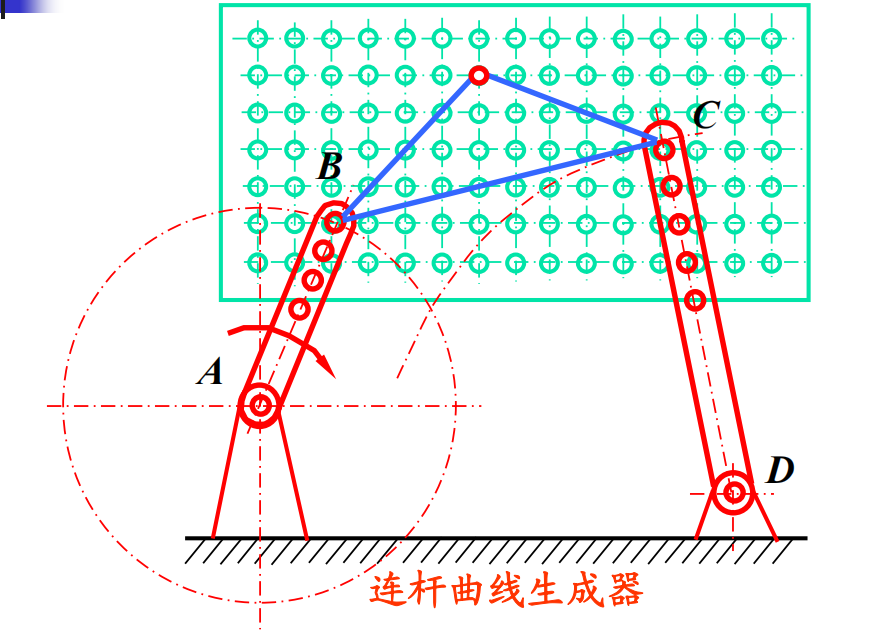
- 给定轨迹：连杆曲线图谱
  
  罗培兹定理

凸轮机构的应用及分类

特点
- 运动规律自由、点或线接触、接触应力高。
分类
- 按凸轮形状分：盘形、移动、圆柱。
- 按从动件的运动分：直动、摆动。
- 按从动件底型式分：尖底、滚子、平底。
- 按高副的锁合方式分：力锁合、几何锁合。
- 其它：等宽凸轮、等径凸轮、共轭凸轮。

偏置直动尖底从动件凸轮机构中的几个术语：

基圆半径($r_0$) 推程(Φ) 远休止(Φs) 回程(Φ’) 近休止(Φs’)

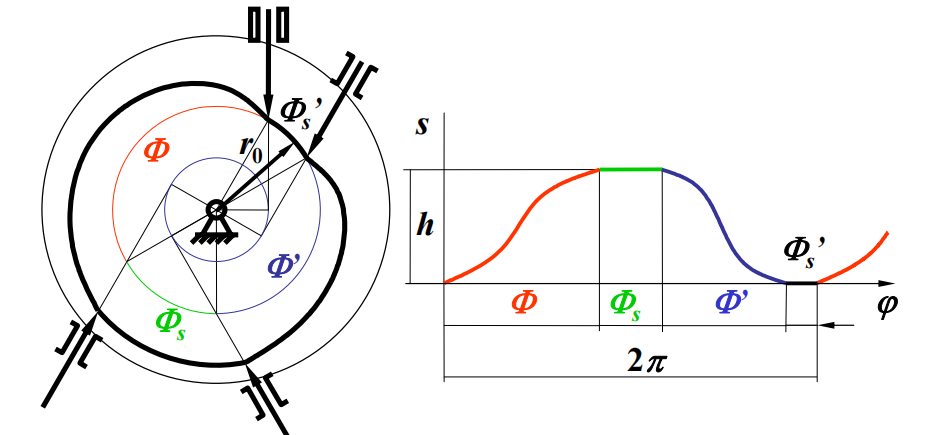
避免刚性冲击：当速度发生突变时，加速度会趋于∞

齿轮

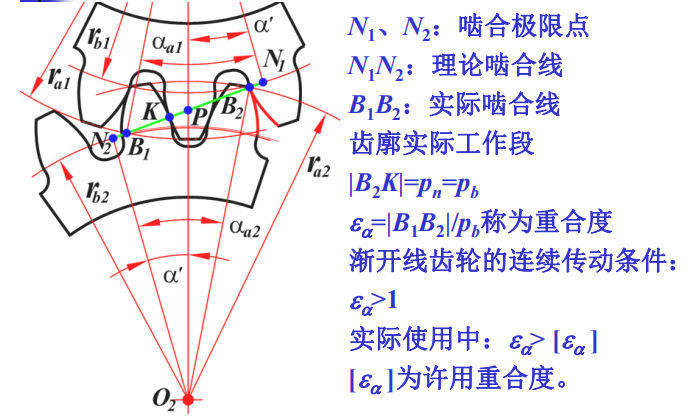
齿廓啮合的基本定理

齿廓啮合基本定律：相互啮合的一对齿廓，在任一位置的传动比，都等于其连心线被过啮合点的公法线所分两线段的反比。

啮合点

$$ i_{12}=\frac{\omega_1}{\omega_2}=\frac{|O_2P|}{|O_1P|} $$

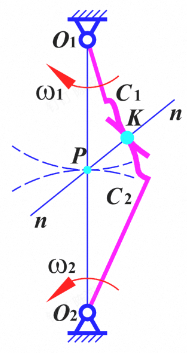
因为所示的P点为两个杆件（齿轮）的速度瞬心

**定传动比条件：**过啮合点的公法线与两齿轮的连心线交于定点。

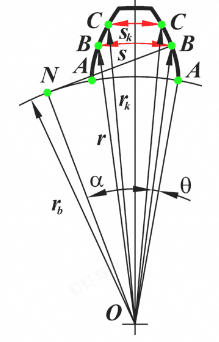
渐开线及渐开线齿廓

渐开线

渐开线的性质
- 想象一根紧绷的绳子缠绕在一个固定的圆柱（称为基圆）上，绳子一端系一支笔。当绳子从基圆上无滑动地匀速展开时，笔尖在平面上画出的轨迹即为渐开线。
- 性质：
  - KB=AB
  - KB与基圆相切
  - B为K点的曲率中心（相当于瞬时转动的圆心）
  - 形状完全由基圆确定
  - 基圆内无渐开线
- 其中的$\alpha$为压力角
- 其中的$\theta$为展角
- 不同位置的向径，压力角，和展角之间有如下的关系式子
  $$ \begin{cases}r_k=r_b/\cos\alpha_k\\\theta_k=\mathrm{tg}\alpha_k-\alpha_k=\mathrm{inv}\alpha_k&\end{cases} $$

主要参数

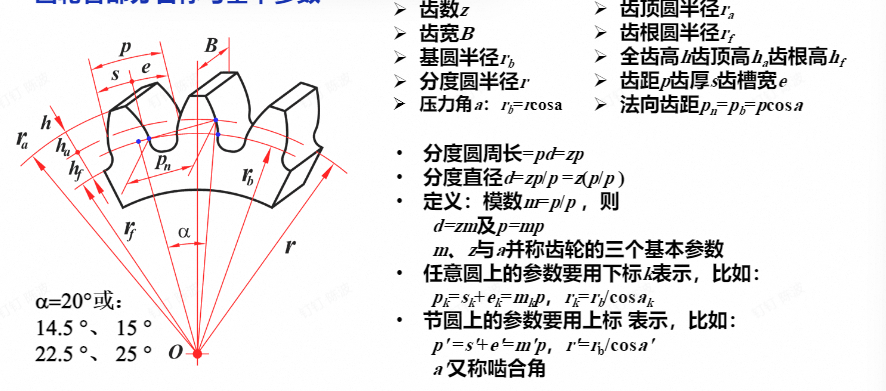
齿数z：有多少个齿
齿宽B：横向的宽度
基圆半径：最开始，画渐开线的基本的圆的半径
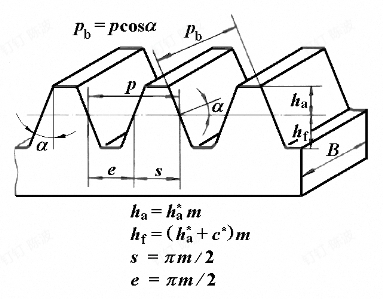
分度圆半径：分度圆上的齿厚（齿的圆周方向厚度）与齿槽宽相等，即$s = e = \frac{\pi m}{2}$（s 为齿厚，e 为齿槽宽）。
压力角：
齿顶圆（根）：最高和最低的圆的半径
全齿高：整个齿从齿顶到齿底的高度
齿顶高：齿顶到分度圆的
齿距p：两个齿之间的距离
齿厚p：齿距是指齿轮上相邻两齿同侧齿廓在分度圆上的弧长。通俗来说，它表示分度圆上相邻两齿对应点之间的圆周距离。
齿厚s:圆截取的齿的长度
齿槽宽e：圆截取的齿之间的长度

角标

任意的圆上的参数使用相同的下标k表示

节圆上的参数使用上标表示`

任意圆上的齿厚：

标准齿条的特点：

什么都没有的是分度圆

有个b的是基圆

m（模数）、z（齿数）、$\alpha$(压力角)为齿轮的三个基本参数

模数相当于齿距除以$\pi$，衡量两个齿之间的距离，齿数衡量齿轮一共有多少个齿数，压力角衡量的是齿的形状（渐开线的形状）

对于一个齿轮在不同的圆上，齿数是固定的。则知道分度圆半径、圆上的压力角，可以求出该圆的半径，求出该圆的模数

分度圆上的齿厚和齿槽宽相等，等于二分之一的齿距

1. 模数（m）

定义：齿距 p 与圆周率 pi 的比值，即 $m = \frac{p}{\pi}$，单位为毫米（mm）。
意义：模数是齿轮尺寸计算的核心参数，模数越大，轮齿尺寸越大，承载能力越强。

2. 齿数（z）

定义：齿轮轮缘上的轮齿总数。
意义：齿数影响齿轮的传动比如一对齿轮传动比 $i = \frac{z_2}{z_1}$和分度圆直径。

3. 分度圆直径（d）

定义：齿轮上用于尺寸计算的基准圆直径，标准齿轮的分度圆上齿厚等于齿槽宽。
公式：$d = m \cdot z$。

4. 齿距（p）

定义：分度圆上相邻两齿同侧齿廓的弧长，$p = \pi \cdot m$。

5. 齿厚（s）与齿槽宽（e）

定义：分度圆上单个轮齿的弧长（s）和齿槽的弧长（e）。
标准齿轮关系：$s = e = \frac{p}{2} = \frac{\pi \cdot m}{2}$

$(\cos\alpha_k = \frac{r_b}{r_k})$
参数	基圆$(r_b）$	分度圆（r）	任意圆$(r_k）$
齿距（p）	$p_b = \pi m \cos\alpha$	$p = \pi m$	$p_k = p \cdot \frac{r_k}{r} = \frac{p_b}{\cos\alpha_k}$
齿厚（s）	$s_b = \frac{\pi m}{2} \cos\alpha（标准齿轮）$	$s = \frac{\pi m}{2}$	$s_k = r_k \left( \frac{s}{r} + 2(\tan\alpha_k - \tan\alpha) \right)$
压力角$\alpha$	$\alpha_b = 0^\circ$	$\alpha = 20^\circ$（标准）	$\cos\alpha_k = \frac{r_b}{r_k}$

标准直齿轮的几何参数

其中的带有的为系数$h{ }$为齿顶高系数，c为顶隙系数，用来计算齿顶高和齿底高

内齿轮的尺寸

$$ d_{\mathrm{a}}=d-2h_{\mathrm{a}}\\d_{\mathrm{f}}=d+2h_{\mathrm{f}} $$

渐开线直齿圆柱齿轮传动

正确啮合的条件

一对齿轮的正确啮合条件是：模数与压力角分别相等。

无隙啮合、标准安装与非标准安装

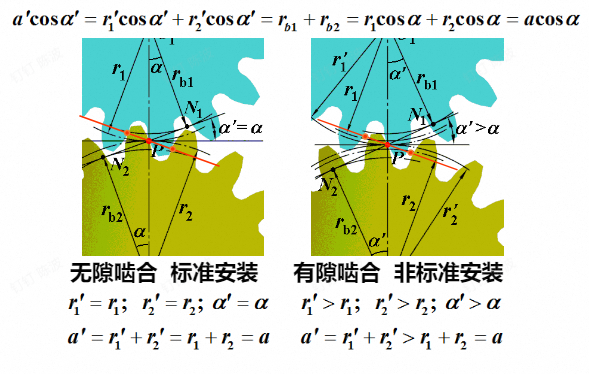
齿轮与齿条啮合时，齿轮的节圆始终与其分度圆重合

标准安装时，齿条与其分度线重合
非标准安装时，齿条和分度选分离
重合度

$$ \varepsilon_\alpha{=}|B_1B_2|/p_b $$$$\begin{array}{l} \varepsilon_{\alpha}=\left(|PB_{1}|+|PB_{2}|\right) / p_{b} \\ =\left[z_{1}\left(\operatorname{tg} \alpha_{1}-\operatorname{tg} \alpha^{\prime}\right)+z_{2}\left(\operatorname{tg} \alpha_{a 2}-\operatorname{tg} \alpha^{\prime}\right)\right] / 2 \pi \\ r_{b}=r \cos \alpha=r_{a} \cos \alpha_{a} \\ \alpha_{a 1}=\arccos\left[\left(r_{1} / r_{a 1}\right) \cos \alpha\right] \\ \alpha_{a 2}=\arccos\left[\left(r_{2} / r_{a 2}\right) \cos \alpha\right] \end{array}$$

当两齿轮的齿数趋向于无穷大时，重合度达到极限：

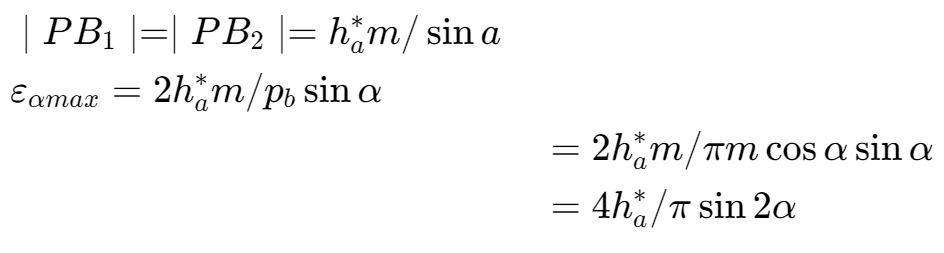
对于标准的直齿圆柱齿轮，有：齿高系数为1，压力角为20°，最大的值为1.981

6-6 渐开线齿轮的加工与根切

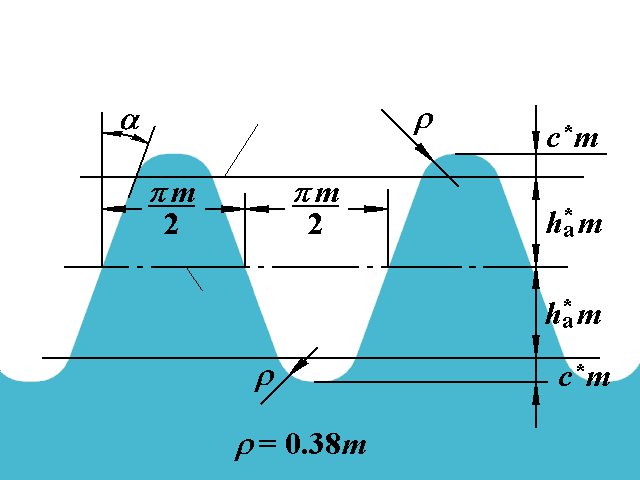
标准齿条的刀具齿形

要使刀具齿顶线落在啮合极限点之下，应有：（齿数的最小值）

$$ z_{\mathrm{min}}=2h_{\mathrm{a}}^{*}/\mathrm{sin}^{2}\alpha $$

变位齿轮及其传动

齿条刀具中线从与齿轮毛坯分度圆相切的位置远离距离xm，将切出变位齿轮。

xm为变位量
x为变为系数
大于0时为正变位
小于零时为负变为
=0时为标准齿轮

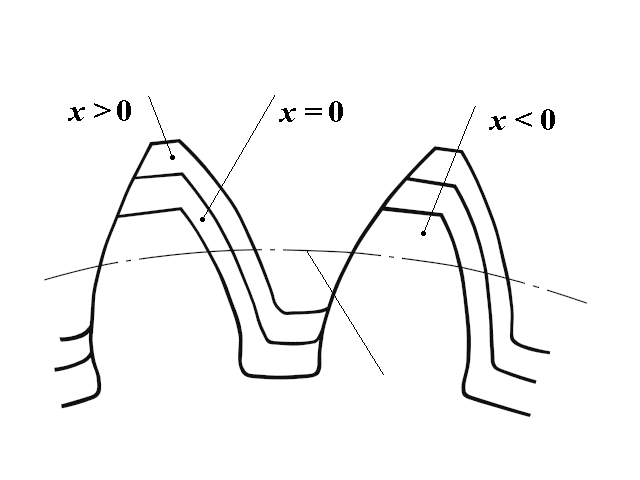
这是变位系数的最小值

$$ x_{\mathrm{min}}=h_{\mathrm{a}}^{*}(z_{\mathrm{min}}-z)/z_{\mathrm{min}} $$

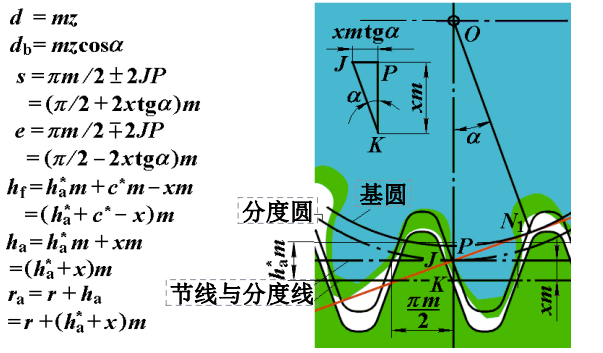
变化之后计算

无隙啮合方程

$$ \mathbf{inv}\alpha^{\prime}=2\mathbf{tg}\alpha(x_{1}+x_{2})/(z_{1}+z_{2})+\mathbf{inv}\alpha $$

计算变为系数和凑出中心距

中心距变动系数y
a为中心距
齿顶高变动系数$\sigma$：将两个轮的齿顶都剪短一些
标注的齿轮传动
高度变位传动
所以等距变位传动的主要优点:z1可以小于最小的z而不产生根切
不等移距变位传动（正传动和负传动）

平行轴斜齿圆柱齿轮传动

参数

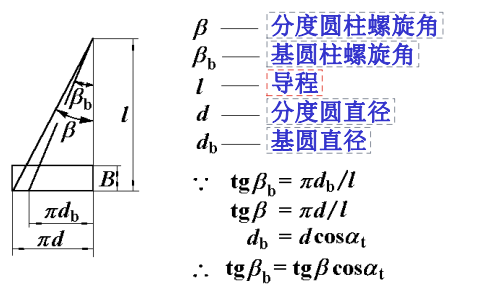
法面参数（加工，受力）
端面参数（与渐开线相关的几何计算）

正确啮合的条件

所以最后的啮合的条件：

圆锥齿轮传动

正确的啮合条件：$m_1=m_2,\alpha_1=\alpha_2$
重合度：按当量齿轮计算
不跟切的最小齿数：$z_{\mathrm{v}}\geq z_{\mathrm{vmin}}=2h_{a}^{*}/\sin^{2}\alpha$

蜗杆的传动

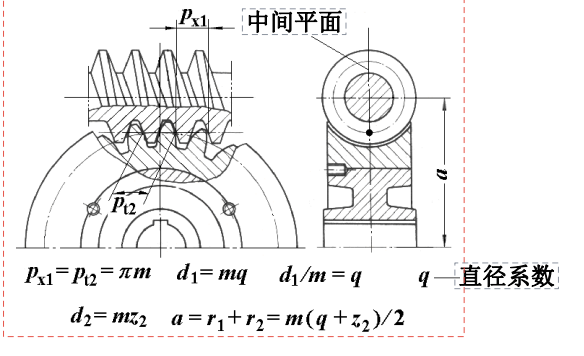
正确的啮合条件：

$$ \gamma_{1}=\beta_{2}\quad m_{t2}=m_{x1}=m\quad\alpha_{t2}=\alpha_{x1}=\alpha $$

主要的参数：

参数1

参数2

重合度

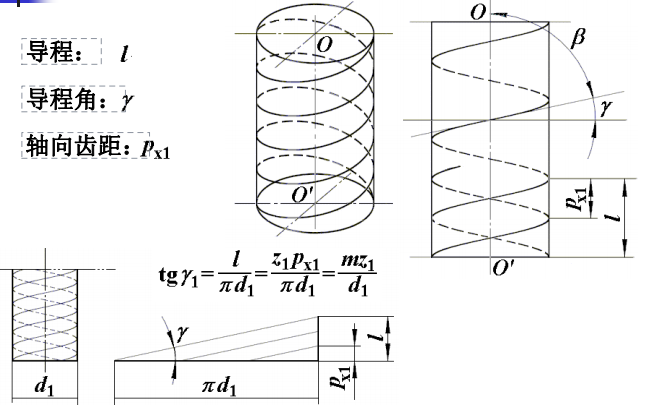
轮系

轮系分类及其应用

分为定轴轮系、周转轮系（齿轮的集合轴线有着公转运动）、复合轮系

定轴轮系的速比计算

轮系的速比定义为：（设A,B分别为轮系的输入轴和输出轴），速比为转速大小的比值，与齿数成反比。

$$ i_{\mathrm{AB}}=\omega_{\mathrm{A}}/\omega_{\mathrm{B}} $$$$ i_{AB}=\frac{\omega_A}{\omega_B}=\frac{\omega_\text{主}}{\omega_\text{从}}=(-1)^m\frac{\text{从动齿轮齿数积}}{\text{主动齿轮齿数积}} $$

其中的m表示内啮合次数（对于轴线平行的，可以选择一个正方向，此时的速比的定义就是一个可正可负的数）

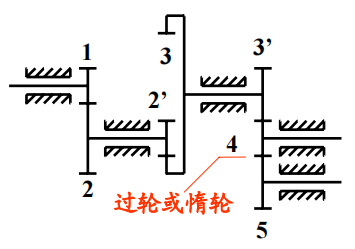
图中的1,2为内啮合，图中的2`,3为外啮合

周转轮系的速比的计算

组成：太阳轮（中心轮），行星架或系杆（转臂H）,行星轮
特征：转换轮系是定轴轮系

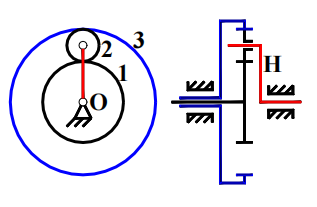
其中的H为行星架，支出的部分使得以它为轴的齿轮的轴是会转动的

转换轮系（周转轮系的速比）

也就是将行星架的速度变为0

所以，有着如下的计算公式：

可以写为速度和齿比的关系，因为转换为了定轴轮系，所以可以使用角速度和齿比计算（任何情况下都可以使用速度的比值列式子，因为是速比）

对于太阳轮的角速度为0时，有如下的原来轮系和转换轮系的速比关系：

上面的角标表示该机构的转速是0的情况下（其中的B为速度为0的太阳轮）

实际上就是将所求的转换为上面带着H角标的（因为带着H角标的是定轴的轮系，可以使用齿数进行计算）

小结论：

因为有几何关系可以看出：分度圆的半径是相等的，并且由于能够啮合，所以模数是相等的，所以最后就可以推出齿数是相等的。（这是隐含的几何条件）

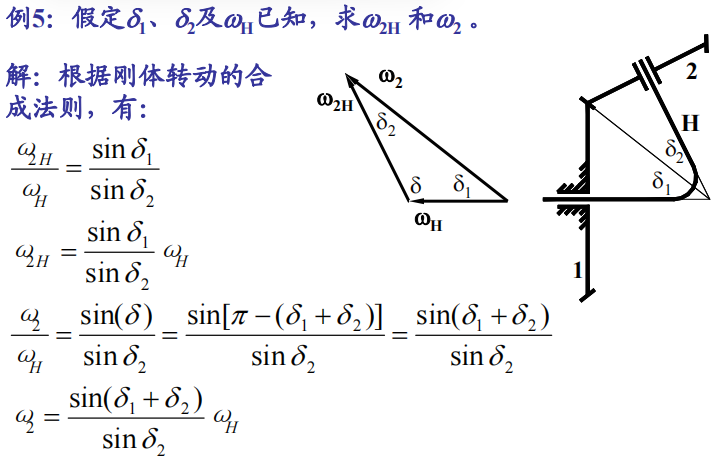
速度的合成

速比之间有着如下的换算：

$$ i_{14}=\frac{i_{1H}}{i_{4H}}=-588 $$
角标相反的速比互为导数

一般选择不转的太阳轮作为换算的依据

复合轮系的速比的计算

步骤：

找出定轴轮系，列出相应的速比方程

找出所有的行星架，对于每个行星架，找出其转换轮系中的定轴轮系，列出速比方程（实际上就是找出周转的轮系）

分析轮系之间的关系，找出公用的构件，建立方程

联立求解

采用乘积的形式列式子，最后转变为都带着行星架的

行星轮系的啮合效率

行星轮系的设计

速比条件：
$$ \boldsymbol{i}_{1H}=\boldsymbol{1}-\boldsymbol{i}_{13}^{H}=\boldsymbol{1}+\frac{z_{3}}{z_{1}}\quad z_{3}=(\boldsymbol{i}_{1H}-\boldsymbol{1})z_{1} $$
同心条件：
$$ \frac{m}{2}(z_1+z_2)=\frac{m}{2}(z_3-z_2)\quad z_2=\frac{z_1}{2}(i_{1H}-2) $$
装配条件：
$$ \begin{aligned}&\frac{2\pi}{k}i_{1H}=\gamma\frac{2\pi}{z_1}\\&\gamma=\frac{z_1}{k}i_{1H}\end{aligned} $$

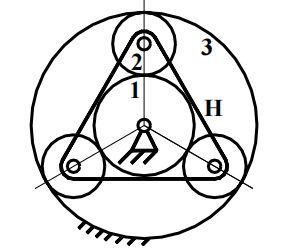
领接条件：
$$ 2(r_1+r_2)\sin\frac{\pi}{k}>2(r_2+h_a) $$$$ z_2<\frac{z_1\sin\frac{\pi}{k}-2h_a^*}{1-\sin\frac{\pi}{k}} $$

如图所示的图

习题课

结构分析

高副低代：

找出接触点在两个接触物体的曲率圆心，连接两个曲率圆心，为增加的杆件

当有多个点在同一个构件上时，使用阴影（剖面线）画出

运动分析

连杆机构的运动分析：

尽量选择速度已知的点，必要时候可以将构件扩大

使用相似三角形分析时：画出来的图形不能翻转，也就是不能镜像

压力角为执行机构的受力与运动的夹角

轮系的分析

做题

轮系中首先要分出周转轮系和定轴轮系

周转轮系的组成是行星轮、太阳轮、架子。要分析清楚哪些的轴是会动的，这些动的轴是在哪个轮上，这个轮就是架子。而动的轮系啮合的不动的轮就是恒星轮

还要注意图中的一些几何关系，（主要是等高的原则）——比如两个齿轮是定轴的，而且齿轮的边缘是对齐的，可以得到一些关系；还有恒星轮是定轴的，上面的行星轮是定轴的，也可以得到一些关系

周转轮系是从太阳轮开始到太阳轮＋行星架，不能反向，只能朝着一个固定的方向走,只有那种短横杆相接的才可以延续下去（还有直接使用实线相连的意味着转速完全相同）

还有就是非平行轴的正负怎么确定

第一题
- 首先是在点上，做基圆的切线，压力角在切点圆心的连线和向径的夹角。展角是起始点（交点）与圆心的连线和向径的夹角
- 分清楚曲率半径（切线的长度）、基圆的半径，向径（圆心连线的长度）
- 计算机按的时候使用的是角度值（°）
- 计算展角的时候：记住由于是一个渐开线，所以有着曲率半径等于圆上的弧长的关系，计算机上算出来的是不是弧度的，所以需要换算成弧度计算（除以180乘以pi）
第二题
- 模数$m =$ \frac{p}{\pi}$$，这里的齿距p指的是分度圆上的齿距
- 分度圆上隐含着齿宽是齿距的一半的隐含条件
- 算齿宽的那个非常长的公式，用的是分度圆上的s
- 在知道齿数的情况下，知道半径、周长、齿距、模数的其一就能知道其余的参数。
- 角度的值与半径和基圆的半径的比值有关，基圆对应的角度为0
- 齿顶高和齿根高是分度圆和齿顶圆、齿根圆的之间的距离
- 主要还是把那些公式记下来，还有就是分清上这些
三
- 防止根切时，正常的齿条形状的齿轮，渐开线始于基圆，为根切的临界点，此时，x带入最小的那个公式
- 标注齿轮
- 要求刚好不跟切
- 转速不同，反求变位系数
四
- 齿数是不变的
- 中心距有变化的公式
- 压力角有变化的公式。加``的为实际的中心距
- 变位系数的计算公式
- 实际顶隙的计算
- 计算两个之间的差值

水木观筹

渐开线的齿廓

分度圆是假象的圆，d=mz

渐开线的轮廓

渐开线是什么？

一直线沿着圆周作纯滚动，，直线上的任意一点的轨迹（选择一个点）
渐开线上一点的压力角：
- $cos\alpha _k=\frac{r_b}{r_k}$任意圆的压力角的公式
- a：齿顶
- f：齿根
- b：基圆
- 不带角标：分度圆（标准的齿轮的为20°）
- 基圆的压力角为0°
展角：$\theta$
- 发生线上的长度等于基圆上滚过的弧长
- 为压力角的正切减去压力角（弧度制）
- 展角的大小为渐开线函数
渐开线的特性：

渐开线的基本参数和几何尺寸

重合度
- 公式：

$$ \varepsilon_\alpha=\frac{\mid B_1B_2\mid}{p_b}=\frac{1}{2\pi}[z_1(\tan\alpha_\alpha-\tan\alpha^{\prime})+z_2(\tan\alpha_\alpha-\tan\alpha^{\prime})] $$

其中的$\alpha^`$为啮合角，对于标准的来说，是等于分度圆上的压力角20°
- 物理含义是实际的啮合比上法向的齿距
基本参数：
- 压力角的公式
- 渐开线函数
- 啮合角和中心距的关系（带`的为实际的中心距）
- 中心距，为模数乘以两个齿数的均值
直齿
- d=mz
- ha=ha*·m
- hf=(ha*+c*)m
- df=d-2hf(齿根圆的直径)
- db=f$cos\alpha$
- p=$\pi m$
- 齿厚和齿
- 任意圆的齿距
- 任意圆的齿厚公式
变位的
- s=
- e=
  - 这两个是怎么来的呢
  - 不产生根切的最小的齿数为$z_{min}$
  - 因为是变位变来的
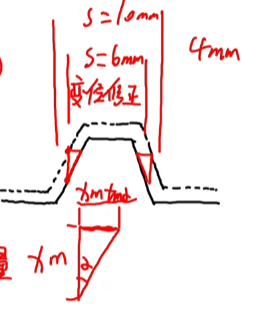
- 变位的系数之和：$x_1+x_2$
一对变位齿轮的变位传动：
- 中心距变动系数y=(a`-a)/m
- 齿顶高降低系数：$\Delta y=x_1+x_2-y$
- 齿顶高也是变了：ha
- 对于单个变为齿轮来说
  - 齿顶高的变化
  - 齿根高的变化

做题

保证能够连续传动：重合度>1
将啮合角计算出来
中心距和啮合角有关系

现将和分度圆有关的计算出来（有模数的时候）

将基圆计算出来（基圆的半径计算出来）

齿顶、齿底的半径等于基圆的加上齿顶、齿底的高

曲率半径直接使用那个勾股定理即可

已知中心距的设计

先确定啮合叫

确定变位系数，就是两个x和的那个公式

计算y和△y

使用上述计算的参数计算基本的参数

使用变