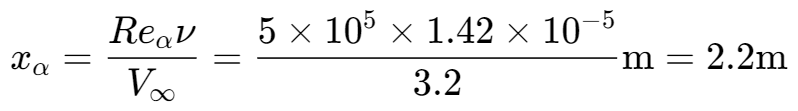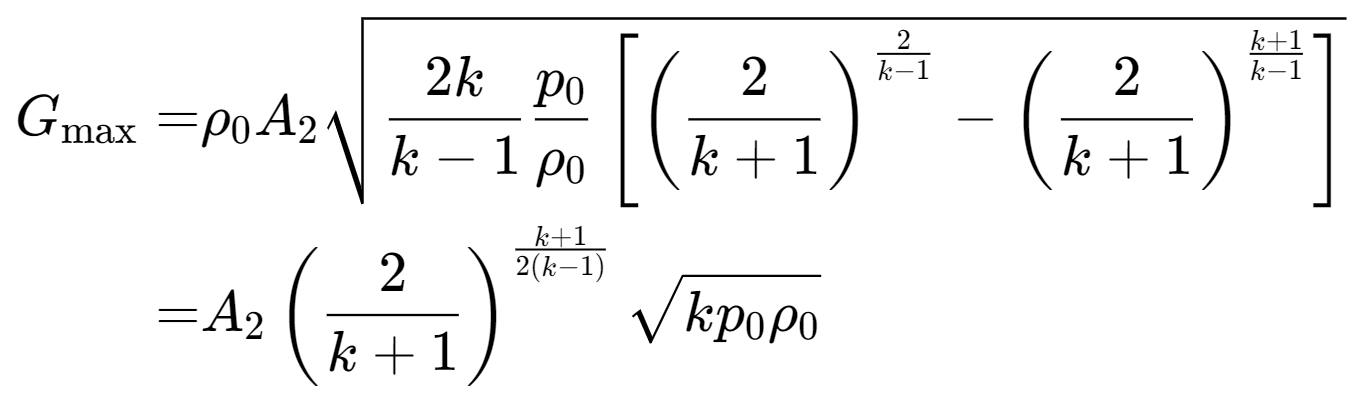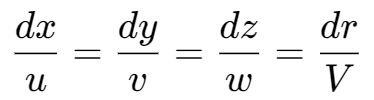流体静力学
静止状态
静止或者是相对静止的流体,质点之间没有相对运动,粘性表现不出来,剪应力为0。
- 静止流体质点间只存在正应力,以压应力的形式体现
- 静止是压应力与体积力相互平衡的结果
静压强的特性:
- 各向等值——点性质,与方向无关
- 作用垂向性——总是作用于物体表面法向
欧拉平衡方程:
$$ f_x = \frac{1}{\rho} \frac{\partial p}{\partial x} = 0\\[6pt] f_y - \frac{1}{\rho} \frac{\partial p}{\partial y} = 0\\[6pt] f_z - \frac{1}{\rho} \frac{\partial p}{\partial z} = 0\\dp=\frac{\partial p}{\partial x}dx+\frac{\partial p}{\partial y}dy+\frac{\partial p}{\partial z}dz=\rho(f_xdx+f_ydy+f_zdz) $$绝对压强、相对压强、真空压强
- 绝对压强:以真空压强(0)为基准的压强
- 相对压强(表压):以大气压强为基准的压强
- 真空压强:当绝对压强小于大气压时,其差值为真空压强(负表压的绝对值)
静水压
**静止状态:**在连续、均匀、静止流体中,压强只和垂直高度相关,与容器形状无关,水平面上压强相等
有加速度情况下的静压强
$$ > \begin{aligned} > & \nabla P=\rho(\mathbf{g}-\mathbf{a}) \\ > & \theta=\tan^{-1}\frac{a_x}{g+a_z} > \end{aligned} > $$
- 压强增加率要大于无加速度情况
- 与容器大小与形状无关
- 等压面平行于自由面
对于一般的情况:
$$ dp=\rho(-adx-gdz),两端积分\\ p=\rho g(-\frac{a}{g}x-z)+c\\ 将坐标原点选在自由面的中心\\ p=p=\rho g(-\frac{a}{g}x-z)+p_a $$有旋转情况下的静压强
$$ p=p_0-\rho gz+\frac{1}{2}\rho r^2\omega^2 $$壁面处液面升高相对于原来的水平面为h/2
相似原理与量纲分析
相似原理
按照相似性原理与量纲分析设计模型,选择流动的介质
相似条件
-
几何相似
-
运动相似
-
动力相似
-
相似判据:
取各种力与惯性力的比值,得到雷诺数,如下:
$$ Re=\frac{F_1}{F_\tau}=\frac{uL}{v} $$雷诺数就是两个流动粘性力相似的判据
将表中的无量纲数统称为相似准则数
流动相似的充分必要条件:
几何相似,运动相似和动力相似
或者满足以下的单值条件:几何、物理、边界、初始条件
量纲分析
量纲和谐原理
物理方程式中的各项必须量纲完全一致。只有相同量纲的物理量才能相加减。
对于相同量纲齐次的方程,只要使用方程的任一量纲除其他各项,变成无量纲量
量纲分析的方法
- 基本的量纲:L,T,M,$\theta$
- 瑞利法
- 列出所有印象这一物理过程的全部n+1个物理量,基本量纲的乘除
- 解出方程
- $\pi$定理
- 组成无量纲的数(选择r个量纲不同的物理量,与其余的物理量组成无量纲数)(一共有k-r个$\pi$数)
- 重复变量与其余变量
- 其中的重复的变量必须是包括所有的量纲的,组成的指数行行列式不为0
模型实验
全面力学相似模型试验
要达到全面的相似,必须所有的相似准则相等,且初始的条件和边界条件相相似。但是这是不现实的
所以在正常的生产中选择主要的因素,使其相等
近似莫化法
抓住主要的矛盾
不可压缩流体的外部流动
边界层的基本概念
基本概念
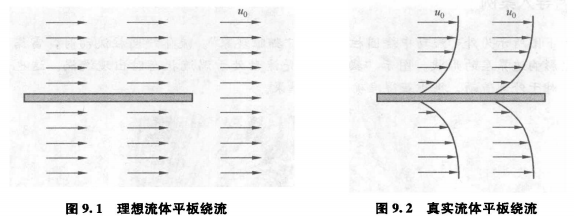
右图的为真实气体的绕流
把这种大Re数下流体绕流物体表面的速度梯度变化很大的薄层称为边界层(boundarylayer)。在边界层以外,由于速度梯度甚小,故其中粘性切应力甚微,因此可视为理想流体。
所以,在大雷诺数的情况下,很薄的层为边界层(速度变化非常快),粘性力的作用明显,但是在边界层之外,粘性的切应力很小,可以看做是理想气体
边界层厚度$\delta$:到达流体来流速度的99%处到平板的距离
边界层理论的意义:
- 当雷诺数很大时,可以将物体表面的流场分为边界层流动和边界层外的势流流动
- 对于边界层,使用边界层方程进行求解
- 对于势流流动,使用理想流体的欧拉方程求解
- 对于小雷诺数时,惯性项远小于粘性项,可以忽略惯性项,简化
基本特征
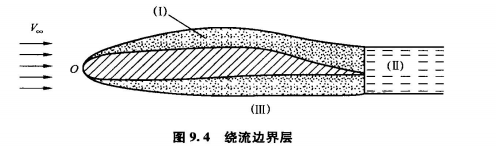
图中的流场分为三个区域:
- 边界层
- 尾流区
- 外部势流
- 对于小雷诺数的情况,边界层较厚,且向前延伸
- 对于大雷诺数的情况,边界层很薄,边界层内的速度梯度很大,粘性切应力很大;外部的速度梯度很小,粘性切应力很小
边界层内存在两种流态:层流边界层和湍流边界层
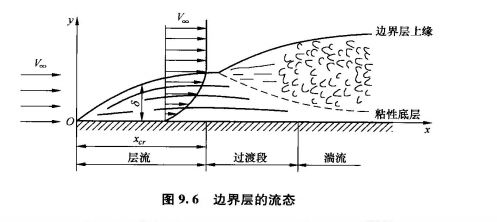
- 判断层流还是湍流的方式:
其中的x为离物体的前段的距离,V为势流速度
对于平板边界层来说:临界的雷诺数为$Re_{x}=3\times10^{5}\sim3\times10^{6}。$
综上所述,边界层的基本特征为:
- 与物体的特征长度L相比,边界层的厚度8很小,即&/L=1;
- 边界层内沿物面法向的速度变化剧烈,即速度梯度au/ay很大;
- 边界层内粘性力和惯性力为同一数量级;
- 边界层沿流动方向逐渐增厚;
- 边界层流体的流动也分为层流和湍流两种流态,用Reg数判别;
- 边界层内压强p与y无关即p=p(x),故边界层各横截面上的压强等于同一截面上边界层外边界上的压强。
边界层微分方程
理想流体的区域可以使用之前的6章中的位势理论求解
但是,边界层内的粘性流体的流动怎么解决
- 方程为:
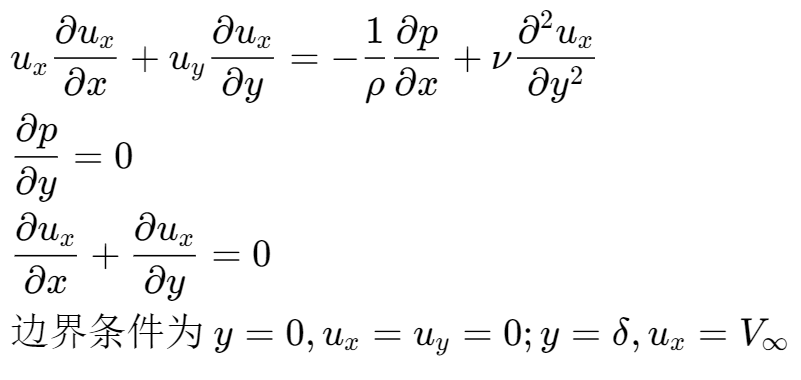
上述的方程可以简化为:
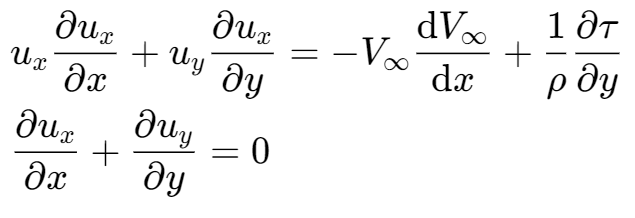
边界层的动量积分方程
由于上述的方程求解起来还是较为困难
- $$ \frac{\mathrm{d}}{\mathrm{d}x}\int_{0}^{s}\rho u_{x}^{2}\mathrm{d}y-V_{\infty}\frac{\mathrm{d}}{\mathrm{d}x}\int_{0}^{s}\rho u_{x}\mathrm{d}y=-\delta\frac{\mathrm{d}p}{\mathrm{d}x}-\tau_{0} $$
- $$ \frac{\partial}{\partial t}\int_{0}^{s}\rho u_{x}\mathrm{d}y+\frac{\mathrm{d}}{\mathrm{d}x}\int_{0}^{s}\rho u_{x}^{2}\mathrm{d}y-V_{\infty}\frac{\mathrm{d}}{\mathrm{d}x}\int_{0}^{s}\rho u_{x}\mathrm{d}y=-\delta\frac{\mathrm{d}p}{\mathrm{d}x}-\tau_{0} $$
平板边界层的近似计算
层流的平板边界层
- $$ \delta=\sqrt{\frac{280}{13}\frac{\mu x}{V_{\infty}}}=4.64xRe_{x}^{-\frac{1}{2}} $$
- $$ u_{x}(y)=V_{\infty}(0.323x^{-1}yRe_{x}^{\frac{1}{2}}-0.005x^{-3}y^{3}Re_{x}^{\frac{3}{2}}) $$
- $$ \tau_{0}=\frac{3\mu V_{\infty}}{2\times4.64\sqrt{\nu x/V_{\infty}}}=0.323\sqrt{\frac{\mu\rho V_{\infty}^{2}}{x}}=0.323\rho V_{\infty}^{2}Re_{\mathrm{L}}^{-\frac{1}{2}} $$
- $$ F_{t}=b\int_{0}^{L}\tau_{0}\mathrm{d}x=0.323b\int_{0}^{L}\sqrt{\frac{\mu\rho V_{\infty}^{3}}{x}}\mathrm{d}x=0.646bL\rho V_{\infty}^{2}Re_{\mathrm{L}}^{-\frac{1}{2}} $$
- $$ C_{1}=\frac{F_{1}}{\frac{1}{2}\rho V_{\infty}^{2}A} $$$$ C_{\mathrm{f}}=1.292Re_{\mathrm{L}}^{-\frac{1}{2}} $$
湍流的
- $$ \delta=0.37\left(\frac{\nu}{V_{\infty}}\right)^{\frac{1}{5}}x^{\frac{4}{5}}=0.37xRe_{x}^{-\frac{1}{5}} $$
-
$$
\delta=0.37\left(\frac{\nu}{V_{\infty}}\right)^{\frac{1}{5}}x^{\frac{4}{5}}=0.37xRe_{x}^{-\frac{1}{5}}
$$$$
\tau_{0}=0.225\rho V_{\infty}^{2}\left(\frac{\nu}{V_{\infty}}\right)^{\frac{1}{4}}\left(0.37\left(\frac{\nu}{V_{\infty}}\right)^{\frac{1}{5}}x^{\frac{4}{5}}\right)^{-\frac{1}{4}}=0.0289\rho V_{\infty}^{2}Re^{-\frac{1}{5}}
$$$$
F_{i}=b\int_{0}^{L}\tau_{0}\mathrm{d}x=0.0289\rho V_{\infty}^{2}\left(\frac{\nu}{V_{\infty}}\right)^{\frac{1}{3}}b\int_{0}^{L}x^{-\frac{1}{5}}\mathrm{d}x=0.036bL\rho V_{\infty}^{2}Re_{\mathrm{L}}^{-\frac{1}{5}}
$$$$
C_{\mathrm{f}}=\frac{0.455}{(\mathrm{lg}Re_{\mathrm{L}})^{2.58}}\quad(10^{5}\leqslant Re\leqslant10^{9})
$$
最后的为平板的阻力系数
计算:
判断边界层的流态
计算$x_{cr}$的大小,确定层流和湍流的分界
使用相应的公式进行计算
沿曲面的边界层及分离现象
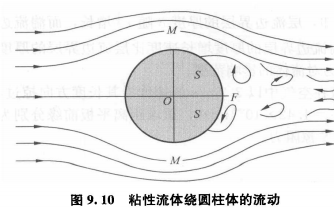
压强的关系:O>F>M
则从O-M是顺压强梯度的流动
但是M-F是逆压强梯度的流动
由边界层理论:
边界层的分离: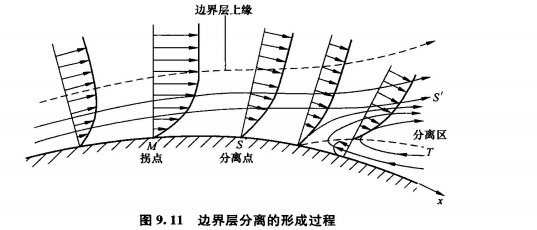
粘性流体绕着小圆球的蠕流流动
斯托克斯阻力系数
在小雷诺数情况下的绕着小球的流动(蠕流)
- $$ u_{r}=V_{\infty}\mathrm{cos}\theta\left[1-\frac{3}{2}\frac{r_{0}}{r}+\frac{1}{2}\frac{r_{0}^{3}}{r^{3}}\right]\\u_{\theta}=V_{\infty}\mathrm{sin}\theta\left[1-\frac{3}{4}\frac{r_{0}}{r}+\frac{1}{4}\frac{r_{0}^{3}}{r^{3}}\right]\\P(r,\theta)=p_{0}-\frac{3}{2}\mu\frac{V_{\infty}r_{0}}{r^{2}}\mathrm{cos}\theta $$
- $$ C_{\mathrm{f}}=\frac{F_{\mathrm{f}}}{\frac{1}{2}\rho V_{\infty}^{2}A}=\frac{6\pi\mu r_{0}V_{\infty}}{\frac{1}{2}\rho V_{\infty}^{2}\pi r_{0}^{2}}=\frac{24}{\frac{V_{\infty}d_{0}}{\nu}}=\frac{24}{Re} $$
颗粒在静止流体中的自由沉降
-
$$
V_{t}=\sqrt{\frac{4gd(\rho_{s}-\rho)}{3C_{t}\rho}}
$$
- $$ V_{\mathrm{f}}=\frac{1}{18}\frac{g}{v}\frac{\rho_{s}-\rho}{\rho}d^{2} $$
- $$ C_{\mathrm{f}}=\frac{24}{Re}+\frac{6}{\sqrt{Re}}+0.4\\0.4V_{\mathrm{f}}^{2}+6\sqrt{\frac{vV_{\mathrm{f}}^{3}}{d}}+\frac{24v}{d}V_{\mathrm{f}}-\frac{4}{3}gd\frac{\rho_{s}-\rho}{\rho}=0 $$
- $$ V_{\mathrm{f}}=\sqrt{2.8gd}\frac{\rho_{s}-\rho}{\rho} $$
粘性物体绕流的阻力
摩擦阻力和压差阻力
绕流阻力由摩擦阻力和压差阻力组成
$$ F_{\mathrm{D}}=(C_{\mathrm{f}}A_{\mathrm{f}}+C_{\mathrm{p}}A_{\mathrm{p}})\frac{\rho V_{\infty}^{2}}{2}\quad\text{或}\quad F=C_{\mathrm{D}}\frac{\rho V_{\infty}^{2}}{2}A $$$C_D$称为绕流系数
绕流物体的升力
$$ F_L=C_L\rho\frac{V^2}{2}A $$$$ \begin{aligned}&\text{式中:}C_L\text{为升力系数}(\text{lift coefficient})\text{,升力系数主要依赖于冲角和物体的横截面的形状;}\\&A\text{ 为物体或升力矢量体的投影面。}\end{aligned} $$做题的感悟:
- 带公式就行
- 主要记住与雷诺数、切应力等等相关的公式
可压缩流体的一维流动
音速和马赫数
音速
$$ c=\sqrt{\frac{\mathrm{d}p}{\mathrm{d}\rho}}=\sqrt{k\frac{p}{\rho}}=\sqrt{kRT} $$上述为音速的计算公式,其中的R为空气的287,k=1.4,这里的温度T在喷管中是会时刻变化的量。
$$ \begin{aligned}&E_{v}=\frac{\mathrm{d}p}{\mathrm{d}\rho/\rho}\\\\&c=\sqrt{\frac{\mathrm{d}p}{\mathrm{d}\rho}}=\sqrt{\frac{E_{v}}{\rho}}\end{aligned} $$不可压缩时,气体的音速将变为无穷大
马赫数
$$ Ma=\frac{V}{a} $$马赫数越小,气体的压缩性的影响就越小,反之,压缩性的影响越大
$( 1) Ma< 1, 则$ $v< c, 气 流 本 身 的 速 度 小 于 声 速 , 为 亚 音 速 流 动 ( subsonicflows) ;$
$( 2) Ma> 1, 则$ $v> c$,气流本身的速度大于声速,为超音速流动(supersonic flows);
$(3)Ma\approx1,则v=c$,气流本身的速度等于声速,称为跨音速流动(sonic flows)。
气体的一维定常流动的基本方程
连续性方程
$$ \frac{\mathrm{d}\rho}{\rho}+\frac{\mathrm{d}v}{v}+\frac{\mathrm{d}A}{A}=0 $$表明速度,密度,流管的截面积三者的相对的变化量的代数和必须为0
能量方程
- 不可压缩流动的
- 省去比位能,加入能量的转换 $$ u+\frac{p}{\rho}+\frac{v^{2}}{2}=C $$
运动方程
$$ \int\frac{\mathrm{d}p}{\rho}+\frac{v^2}{2}=C $$定常流动的基本特性
滞止状态
$$ \begin{gathered}h_{0}=h+\frac{v^{2}}{2}\\C_{p}T_{0}=C_{p}T+\frac{v^{2}}{2}\\\frac{k}{k-1}\frac{p_{0}}{\rho_{0}}=\frac{k}{k-1}\frac{p}{\rho}+\frac{v^{2}}{2}\\\frac{k}{k-1}RT_{0}=\frac{kRT}{k-1}+\frac{v^{2}}{2}\\\frac{c_{0}^{2}}{k-1}=\frac{c^{2}}{k-1}+\frac{v^{2}}{2}\end{gathered} $$流动速度为0的点的状态为滞止状态,角标使用0表示
注意区分这里的c和v:c是代表此点的温度下对应的声速,v是代表气体的流速,是有区别的
临界状态
$$ \frac{T^{*}}{T_{0}}=\left(1+\frac{k-1}{2}\right)^{-1}=\left(\frac{2}{k+1}\right)\\\frac{\rho^{*}}{\rho_{0}}=\left(1+\frac{k-1}{2}\right)^{\frac{-1}{k-1}}=\left(\frac{2}{k+1}\right)^{\frac{1}{k-1}}\\\frac{p^{*}}{p_{0}}=\left(1+\frac{k-1}{2}\right)^{\frac{-k}{k-1}}=\left(\frac{2}{k+1}\right)^{\frac{k}{k-1}} $$断面上的速度为此点对应的的音速时为临界状态,使用角标*表示
公式中的密度的标识为比体积的倒数
极限状态
$$ \frac{c_0^2}{k-1}=\frac{c^2}{k-1}+\frac{v^2}{2} $$由这个能量守恒方程
$$ v_{\mathrm{mex}}=\sqrt{\frac{2}{k-1}}c_{0} $$这时的内能和压能全部位移0,称为达到了极限状态
此时的热力学温度为0,绝对压强为0
喷管中的等熵流动
$$ \frac{\mathrm{d}A}{A}=-\frac{1-Ma^{2}}{kMa^{2}}\frac{\mathrm{d}p}{p} $$
- 亚音速时,只有截面缩小才能使压强降低、温度降低,焓降低,气流加速,截面增大使气流减速
- 超音速时,与上面的相反
- 音速流动时,处于临界的状态
喷管
渐缩喷管
需要求渐缩喷管的出口的流速和流量
- 在已知滞止时的压力和出口的压力的情况下(出口的压强小),出口的流速为
- 流量为 $$ \begin{aligned}\mathrm{G}&=\rho_{2}A_{2}V_{2}\\&=\rho_{0}A_{2}\sqrt{\frac{2k}{k-1}\frac{p_{0}}{\rho_{0}}\left[\left(\frac{p_{2}}{p_{0}}\right)^{\frac{2}{k}}-\left(\frac{p_{2}}{p_{0}}\right)^{\frac{k+1}{k}}\right]}\\&=\rho_{0}\left(\frac{p_{0}}{p_{2}}\right)^{\frac{1}{k}}A_{2}\sqrt{\frac{2k}{k-1}\frac{p_{0}}{\rho_{0}}\left[1-\left(\frac{p_{2}}{p_{0}}\right)^{\frac{k-1}{k}}\right]}\end{aligned} $$
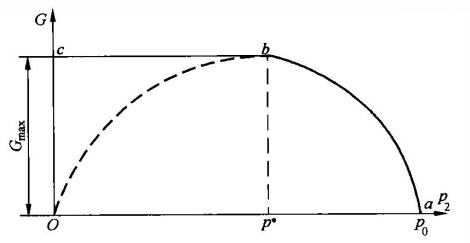
观察公式可以看出:
- 对于流速,出口的压强越小时,出口的流速越大,当出口的压强为0时,达到最大的流速,但是这个流速好像达不到,因为达到临界压强之后,随着面积的减小,压强会变大。
- 对于出口的流量,最大时的压强取值为$p_2=p_0\left(\frac{2}{k+1}\right)^{\frac{k}{k-1}}=p^*$,此时的压强为临界压强,流量达到最大值,出口的速度为音速
- 此时的最大流量为
所以,出口的压力达到临界压力之后,出口压力再降低,流量也保持到最大值不会变化
计算过程
- 计算出口处的压强和滞止压强的比,与临界压强比较,确定是使用渐缩喷管还是缩放喷管
- 计算各状态下的状态参数(带入等熵的公式),利用状态参数的值计算各状态下的流速
- 利用流量和流速计算截面积
一些想法:
- 知道某点的流速和声速的比值,就能知道温度和滞止温度的比值(利用能量方程和声速与温度的关系)
- 然后就能算出状态参数
- 速度和进出口的压强比也有直接的联系
有摩擦的等截面管内的绝热流动
$$ \lambda\frac{L}{D}=\lambda\frac{L_{1}^{*}}{D}-\lambda\frac{L_{2}^{*}}{D}=\frac{Ma_{2}^{2}-Ma_{1}^{2}}{kMa_{1}^{2}Ma_{2}^{2}}+\frac{k+1}{2k}\ln\frac{Ma_{1}^{2}}{Ma_{2}^{2}}\frac{1+\frac{k-1}{2}Ma_{2}^{2}}{1+\frac{k-1}{2}Ma_{1}^{2}} $$上述为临界管长的计算公式(即管子在有摩擦的情况下,能够到达1Ma所需的最短的管子长度)
激波的形成
流动钟流体参数突变的薄层叫做激波
马赫波
超音速流动时,气流的速度大于扰动的传播速度
复习
层流流动的剪应力
$$ \tau=\mu\frac{du}{dy} $$$$ \nu=\frac{\mu}{\rho} $$其中的$\mu$为粘度
运动粘度和粘度之间的关系,差个密度的倍数
非牛顿流体
流体静力学
特性
各向等值性 —点性质(point property),与方向无关
作用垂向性—总是作用于物体表面法向
压强变化最大的方向沿着重力方向
压强等值面垂直于重力方向
相邻的截面上的等高处的压强相等
取几个截面(一般以不同的液面为分界)
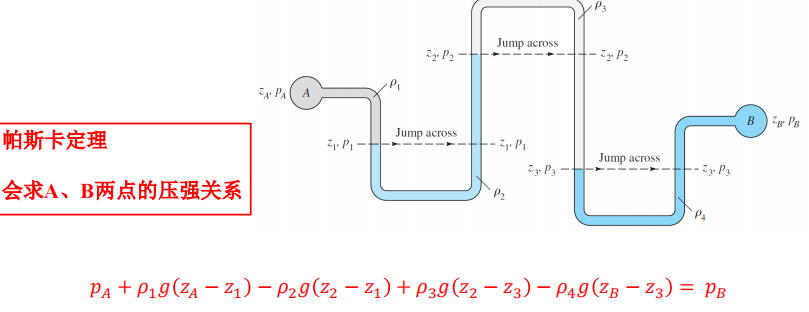
有加速度情况下的
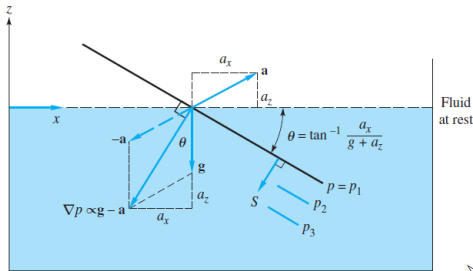
- 压强的增加率大于无加速度的情况
- 与容器的大小和形状无关
浸没平壁的受力分析
-
作用于平壁面的总压力等于其形心压强乘以面积
-
作用点位于
-
积分法
- $$ y_{\mathrm{CP}}=-\gamma\sin\theta\frac{I_{xx}}{P_{\mathrm{CG}}A} $$
-
其中的$gamma$为$\rho g$
-
式子中的压强为形心位置的压强
-
$\theta$是和水平面的夹角
-
Ixx为关于形心x轴的二阶惯性矩
- $$ x_{\mathrm{CP}}=-\gamma\sin\theta\frac{I_{xy}}{p_{\mathrm{CG}}A}| $$
-
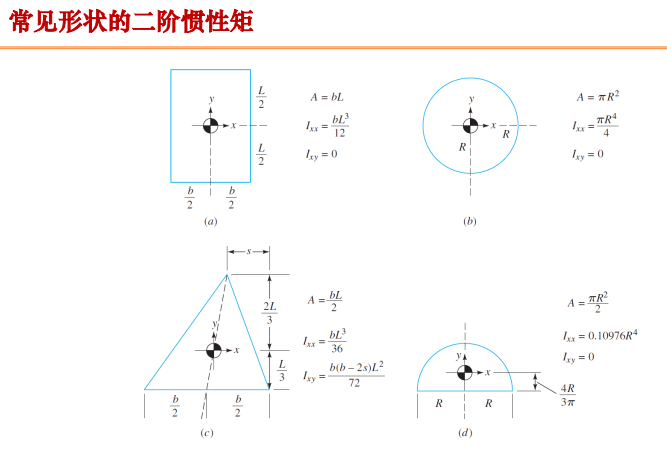
-
流体动力学
流线
- 流线是流场中任一时刻的一条几何曲线,其上各点的速度矢量均与此曲线相切。因此,流线是同一时刻,不同流体质点所组成的曲线。由欧拉法引出。
是不同的流体质点,相当于波形图(固定时刻,但是不固定是哪个点)
特点
- 在定常流中,速度场不随时间改变,即 v t / 0 , 流线簇也不随时间改变 ,用一幅流线图就可以表示出流场的全貌
- 流线密集的地方,表示流场中该处的流速较大,稀疏的地方,表示该处的流速较小
方程
可以由速度求解流线方程
微分形式的质量守恒方程(连续方程)
- 不可压缩的连续性方程
上述为散度的定义
- 线应变的速率
- 体积应变的速率
- 角应变速率
- 旋转角速度
判断流动时有旋的还是无旋的

- 判断不可压缩(连续性)
- 判断有旋
- 判断有无角变形
流体的动力学
- 三维不可压缩牛顿流体的应力分量
系统和控制体
- 受力的控制体分析

欧拉方程
$$ \rho g_x-\frac{\partial p}{\partial x}=\rho\frac{du}{dt}\\\rho g_y-\frac{\partial p}{\partial y}=\rho\frac{d\upsilon}{dt}\\\rho g_z-\frac{\partial p}{\partial z}=\rho\frac{dw}{dt} $$为无粘的情况下的ns方程的简化
流函数
$$ u=\frac{\partial\psi}{\partial y}\quad v=-\frac{\partial\psi}{\partial x} $$求解:
- 是否满足连续性
速度势
如果一个矢量的旋度为零,那么这个矢量可表达为一个标量的梯度

满足无旋流动的条件即可
速度势对某个方向进行微分,等于这个方向的速度分量(求解的方式)
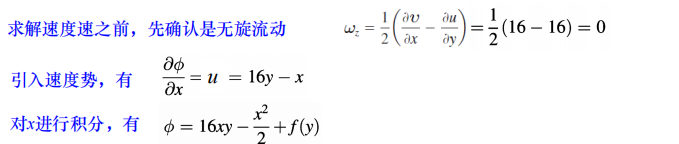
流函数与势函数的性质
- 流函数
- 二维稳态不可压缩流动,有黏无黏都存在流函数
- 流函数满足连续性方程
- 对无旋稳态不可压缩流动,流函数满足拉普拉斯方程
- 速度势
- 只要流动无旋,就存在速度势
- 速度势的梯度是速度
- 对稳态不可压缩流动,速度势和流函数正交
伯努利方程
$$ \frac{p_1}{\rho}+\frac{1}{2}V_1^2+gz_1=\frac{p_2}{\rho}+\frac{1}{2}V_2^2+gz_2=\mathrm{const} $$使用的条件:(使用过的条件还是比较苛刻的)
- 定常
- 不可压缩
- 无粘
- 沿着一条流线
量纲分析
瑞利法
影响因素
其中的一个可以表示为其他的乘积的形式
由量纲分析的原理
分析求出系数
适合比较简单的问题
实际上就是使等式左右的量纲齐次
白金汉定理
选择含有所有的基本量纲的参数(等于基本量纲的数目)
将其余的参数使用这些参数进行表示(实际上就是选择基底进行表示)
不可压缩流体的内部流动
圆管中的层流
- 速度的分布
- 最大的速度
- 流量的大小
- 流速的分布
- 切应力
- 阻力系数
上述的这些对于Re<2300的圆管层流都成立
充分发展
在起始的部分,由于粘性的作用,会存在边界层,随着距离的发展,边界层不断加厚,之后,边界层重合,此时是充分发展的截断(之后的速度分布就不变了,二次曲线的形状)
有着从起始到达充分发展的长度L
圆管湍流运动
水头损失,沿程损失系数
管路的总的水头损失系数为沿程损失系数和局部损失系数的和
todo
- 动量平衡方程那里